Part 2k: Microsoft Binary Format

 At some stage I was going to need to figure out how floating point numbers are stored to help with the disassembly and for my own curiosity.

I know Integer BASICs often stores Integers as twos-complement binary format using 16 bits to represent numbers in the range of -32768 to 32767. It's not too hard to convert those from binary to decimal for the user to read. I think most retro microcomputer enthusiasts and programmers will already be familiar with that to some extent.

However it's a whole different kettle of fish when it come to floating point numbers, and to make it even harder to follow, different methods have been used on different interpreters. It's up to the programmer to some extent how they want to store the numbers unless they have to follow some standard.

If you look up Wikipedia you will find this list of standards:

But which 32-bit standard one do we want ?

IEEE 754 32-bit floating-point standard. Almost but NOT the standard used on the ALTAIR!

Microsoft's Monte Davidoff was the one who came up his own floating-point standard to be used in the 4K and 8K interpreters on the ALTAIR, and since there were no standards back in 1976, he made up his own. He decided on a 32 bit format because it kept the memory usage down and was adequate for floating point representation.

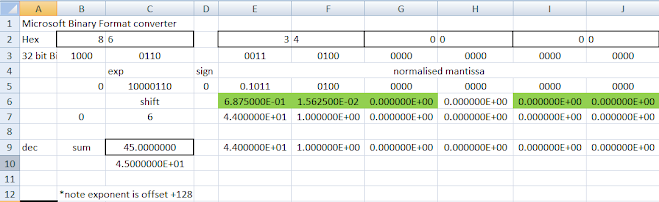
The way ALTAIR BASIC stores the floating point numbers is like this:

Microsoft Binary Format (MBF). Similar to IEEE 754 but different.

There are some examples of Microsoft Binary Format here:

https://en.wikipedia.org/wiki/Microsoft_Binary_Format

Good, but how do I convert other numbers.

I tried unsuccessfully to find an on-line converter for 32 bit MBF but failed. So I had to create my own method instead. I did one or two by hand and it took ages and prone to errors. Eventually I created a spreadsheet that could do a reasonable job of converting from HEX (binary) to decimal, although a bit clunky to use it was much faster and more accurate than my manual attempts:

My own spreadsheet to convert from Hexadecimal (binary) to Decimal. Here we see hexadecimal $86 $34 $00 $00 converts to decimal 45. You can also see the Binary representation under the Hexadecimal.

The reason I need to convert hexadecimal to binary is because throughout the ROM there is apparent blocks of data and I want to know if they are decimal constants and if so what their value is. Once I know that I can then work out where some of the math subroutines are located and how they work (eventually).

This is an example of a random block that looks like it might be data constants:

12B1 : 81 00 "  " cmpa #$00
;
12B3 : 00 " " db $00
12B4 : 00 " " db $00
12B5 : 02 " " db $02
;
12B6 : 80 19 "  " suba #$19
12B8 : 56 "V" rorb
12B9 : AA 80 "  " oraa $80,x
12BB : 76 22 F1 "v" " ror X22F1
12BE : 82 38 " 8" sbca #$38
12C0 : AA 45 " E" oraa $45,x
12C2 : 80 35 " 5" suba #$35
;
12C4 : 04 " " db $04
12C5 : F3 " " db $F3
;
12C6 : 81 35 " 5" cmpa #$35
;
12C8 : 04 " " db $04
12C9 : F3 " " db $F3
;
12CA : 80 80 "  " suba #$80
;
12CC : 00 " " db $00
12CD : 00 " " db $00
;
12CE : 80 31 " 1" suba #$31
;
12D0 : 72 "r" db $72
12D1 : 18 " " db $18

At first glance this looks like garbage or data, certainly not code with all those 'db' declarations.

After some tidying up and MBF conversion it becomes a lot clearer what's stored here:

;********************************************************************
; Data constants section
; Unity
12B1 : 81 00 00 00 X12B1: db $81, $00, $00, $00 ;=1.000000 yes
; LOG series table
12B5 : 02 db $02 ;3 entries in LOG() series
12B6 : 80 19 56 AA X12B5: db $80, $19, $56, $AA ;=0.59897864 yes
12BA : 80 76 22 F1 db $80, $76, $22, $F1 ;=0.96147066 yes
12BE : 82 38 AA 45 db $82, $38, $AA $45 ;=2.8853934 yes
; Other constants
12C2 : 80 35 04 F3 X12C2: db $80, $35, $04, $F3 ;SQR(0.5) =  0.70710677 yes
12C6 : 81 35 04 F3 X12C6: db $81, $35, $04, $F3 ;SQR(2)   =  1.4142135 yes
12CA : 80 80 00 00 X12CA: db $80, $80, $00, $00 ;-1/2     = -0.50000000 yes
12CE : 80 31 72 18 X12CE: db $80, $31, $72, $18 ;Ln(2)    =  0.69314718 (natural log) yes
;********************************************************************

Other Microsoft BASICs have similar constants stored in the ROM for their maths routines. By comparing those to this BASIC allowed me to figure out what the data constant blocks were used for in the math routines. Although sometimes the values differed slightly to those BASICs.

;**********************************************************************
;floating point constants
1881 : 81 49 0F DB db $81, $49, $0F, $DB ;pi/2 = 1.570796 yes
1885 : 83 49 0F DB db $83, $49, $0F, $DB ;2*pi = 6.283185 yes
;(why a 2nd entry for 2*pi)
1889 : 7F 00 00 00 db $7F, $00, $00, $00 ;1/4 = 0.25 yes
;Taylor series used for SIN()
188D : 04 db $04 ;5 coefficients for SIN()

188E : 86 1E D7 BA db $86, $1E, $D7, $BA ; ((2*pi)^9)/9! = 39.710670 yes
1892 : 87 99 26 64 db $87, $99, $26, $64 ;-((2*pi)^7)/7! = -76.574982 yes
1896 : 87 23 34 58 db $87, $23, $34, $58 ; ((2*pi)^5)/5! =  81.602234 yes
189A : 86 A5 5D E0 db $86, $A5, $5D, $E0 ;-((2*pi)^3)/3! = -41.341675 yes
189E : 83 49 0F DA db $83, $49, $0F, $DA ; (2*pi)        =  6.283185 yes
;this section may be overwritten by start of BASIC program data depending on trig option selected
;**********************************************************************

Another block of floating point constants. These ones are used for SIN function and probably for COS and TAN as well.

Armed with this information I may eventually determine how the math routines worked, however I decided that was going to take a lot of time to work out, so most if not all the the math functions have barely any comments other than identifying what location in the memory they occupy.

Entering the math routines was more or less robotic and I was just typing in a lot of blocks of code monotonously. Fortunately there was not a lot of patching to do in those commands.

Next I get some of the bugs out...